-
解析応用編
7. カプランマイヤー法(Kaplan-Meier method)によるイベント発生率の点推定とNumber at riskの算出
このサイトは無料の統計ソフトである「R」を用いて
カプランマイヤー法(Kaplan-Meier method)によるイベント発生率の点推定とNumber at riskの算出が実行できるように説明したサイトです。
「臨床医のためのRコマンダーによる医学統計解析マニュアル」の読者を対象に作成しており、本書の内容を理解しているものとして解説していきます。
イベント発生率の点推定
それでは早速やってみましょう。
まずは「臨床医のためのRコマンダーによる医学統計解析マニュアル」のp102以降を参考に
練習用データを用いて糖尿病の有無による生存率の違いをカプランマイヤー法(Kaplan-Meier method)を用いて描出してみて下さい。
手順に従い実行するとRコマンダーのスクリプトウィンドウには下記のように表示されます。
.Survfit <- survfit(Surv(death_time, death_censor) ~ diabetes, conf.type="log", conf.int=0.95,
type="kaplan-meier", error="greenwood", data=practice)
.Survfit
plot(.Survfit, col=1:2, lty=1:2, conf.int=FALSE, mark.time=TRUE)
legend("bottomleft", legend=c("No","Yes"), title="diabetes", col=1:2, lty=1:2, bty="n")
quantile(.Survfit, quantiles=c(.25,.5,.75))
remove(.Survfit)
やることは一つだけです。
最後の
remove(.Survfit)のremoveをsummaryに書き換えて下さい。
そして再度スクリプトを実行するとRコマンダーの出力ウィンドウ下記のような結果が得られます。
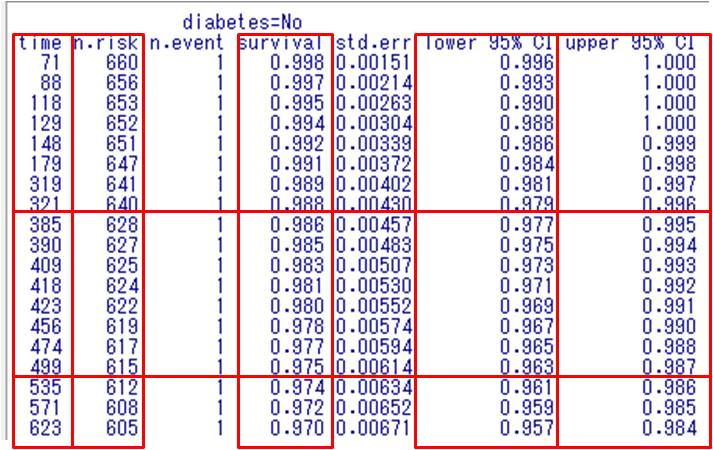
もうおわかりだと思いますが、この結果をみるとある時点における推定生存率とその95%信頼区間、number at risk(=その時点で生存している患者の数)がすべてわかります。
それでは詳しく見て行きましょう。
まずこのデータはタイトルにdiabetes=Noと書いてあることから糖尿病のない患者におけるデータであることがわかります。
次に赤四角で囲った部分を左から見て行きます。
timeは時点を、n.riskはnumber at risk(=その時点で生存している患者の数)を、survivalは生存率を、lower 95%
CIはその95%信頼区間下限値を、upper 95% CIは上限値を意味しています。
死亡率が知りたい場合は1から生存率を引いた値を用いればよいだけです。
Number at riskの算出
次に任意の点におけるNumber at riskの算出方法に関して説明致します。
この計算にはggplot2とsurvminerパッケージを用いると非常に簡単に計算可能です。
まずはこれらのパッケージをインストールして下さい。
次に以下のスクリプトをR Consoleに張り付けて実行します。
ここでスクリプト内青文字部分の「.Survfit」は、上記のカプランマイヤー法(Kaplan-Meier method)で実行されるスクリプトのものになりますので、必ず上記のremoveをsummaryに修正する手順を行った上で以下のスクリプトを実行下さい。
break.time.by=の後の数字は、指定日数ごとのNumber at riskが算出されるという意味ですので、興味のある時点を指定すれば任意の時点におけるNumber
at riskを算出可能です。
#########コピーアンドペースト_ここから##########
library(ggplot2)
library(survminer)
ggsurvplot(.Survfit, break.time.by=365, risk.table=T)
#########コピーアンドペースト_ここまで##########
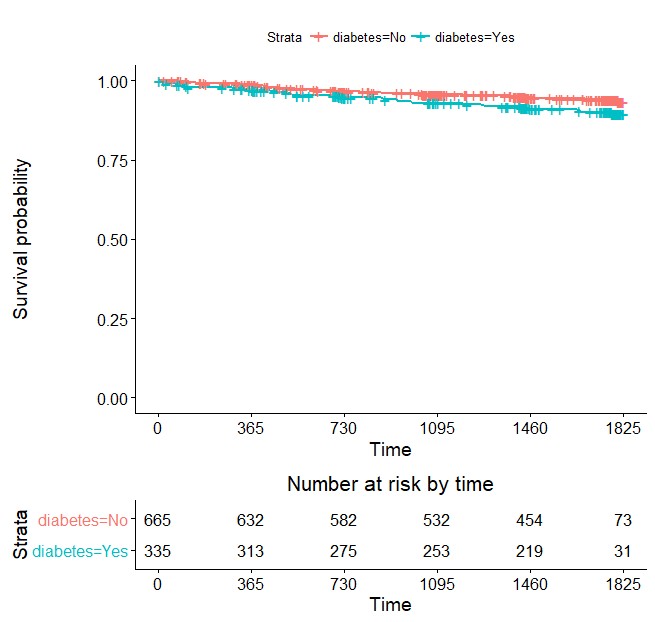
なお、ggsurvplotのメジャーなagumentsは以下の通りです。
コピーアンドペーストして色々と試してみると面白いと思います。
ggsurvplot(.Survfit, col="red", palette=c("blue","green")
, censor=F, break.time.by=365, conf.int=T, risk.table=T
, linetype=1, pval=T, pval.coord=c(365, 0.80), size=1, fun="event",
ylim=c(0,1), xlim=c(0,1825))
1. col/palette
群分けをしない場合はcolで、群分けをする場合にはpaletteで線の色を指定します。数値でも文字でもよいですが、文字で指定する場合にはクォーテーションで囲みます。群分けする場合にはpalette=c(1,2)や、palette=c("blue","green")等と記載します。
2. censor
FALSEでイベントインディケーターを消します。TRUEでイベントインディケーターを表示します。FALSEはF、TRUEはTとのみタイプしても問題ありません。
3. break.time.by
x軸のマーカーの位置を指定します。
4. conf.int
95%信頼区間をTRUEで表示、FALSEで非表示にします。
5. risk.table
Number at riskをTRUEで表示、FALSEで非表示にします。
6. linetype
線のタイプを指定します。数値でも文字でもよいですが、文字で指定する場合にはクォーテーションで囲みます。群分けする場合にはlinetype=c(1,2)や、linetype=c("solid","dashed")等と記載します。
7. pval
群分けする際のログランク検定値を表示します。
8. pval.coord
p値を表記する座標をpval.coord=c(365, 0.80)等の様に指定します。( )内の最初の数字がx軸、後の数字がy軸上の座標になります。
9. size
線の太さを指定します。
10. fun
fun=NULLで一般的なカプランマイヤー曲線を描出します。fun="event"で累積イベント率に変換します。
11. ylim/xlim
y軸、又はx軸の範囲を指定します。