-
解析応用編
5. 交互作用の評価方法 P for interaction、P for trendの算出
このサイトは無料の統計ソフトである「R」を用いて
交互作用の評価方法であるp for interaction、p for trendの算出
が実行できるように説明したサイトです。
「臨床医のためのRコマンダーによる医学統計解析マニュアル」の読者を対象に作成しており、本書の内容を理解しているものとして解説していきます。
その他、臨床研究や英語論文執筆にご興味のある方は無料のメールマガジン
「臨床研究の立ち上げから英語論文発表までを最速最短で行うための極意」への登録も御考慮下さい。
交互作用とは
臨床論文では大規模データを扱う際にサブグループ解析の結果と共に交互作用の検討、すなわちp for interactionやp for trendの算出を求められることがあります。
一般臨床病院で個人的に集めたデータを解析する際にこの知識が必要になることはあまりないと思いますが、大規模なデータを扱う必要性ができた際には役に立つと思いますのでこのページで少し追加説明をさせて頂きます。
まず、医学臨床論文で求められる交互作用の有無の概念ですが、これは簡単に言ってしまうとある治療効果の「ハザード比やオッズ比が、サブグループ間で異なるか」どうかということになります。
例えば、下図は全症例と男性のみのサブグループ、女性のみのサブグループにおいて、治療Aを行うことで死亡率が改善するかどうかをハザード比で検討した結果を示す図です。
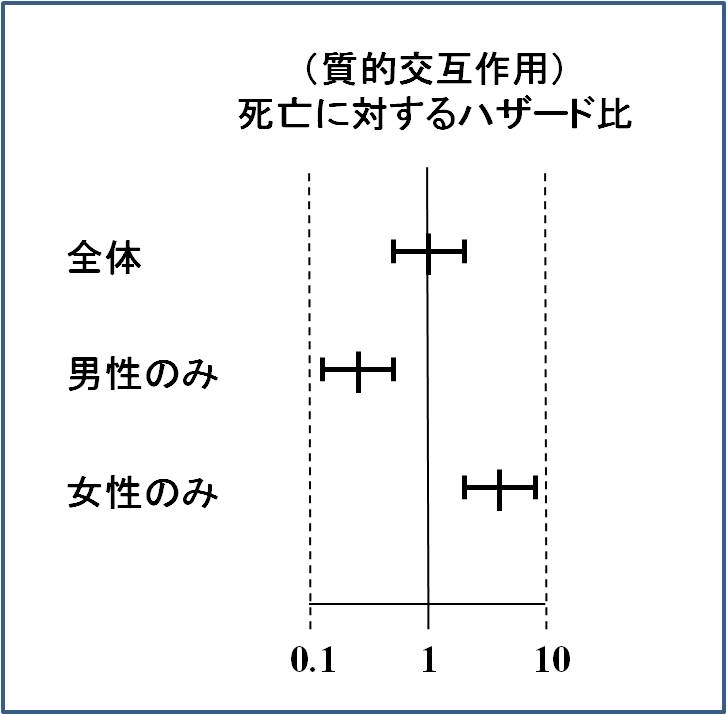
一見全体でみると治療Aに予後改善効果はないように見えますが、実はサブグループ解析によって男性のみの群では有意に死亡率を低下させ、女性のみの群では逆に治療Aが死亡率を上昇させてしまう(有害である)ことが示されています。
このようにサブグループ間である治療が全く逆の効果を示す場合を、質的交互作用 qualitative interactionがあると表現します。
一方で下図のように、治療効果は同じ方向だけれども、その効果の大きさに違いがあるような場合は量的交互作用 quantitative interactionがあると表現します。
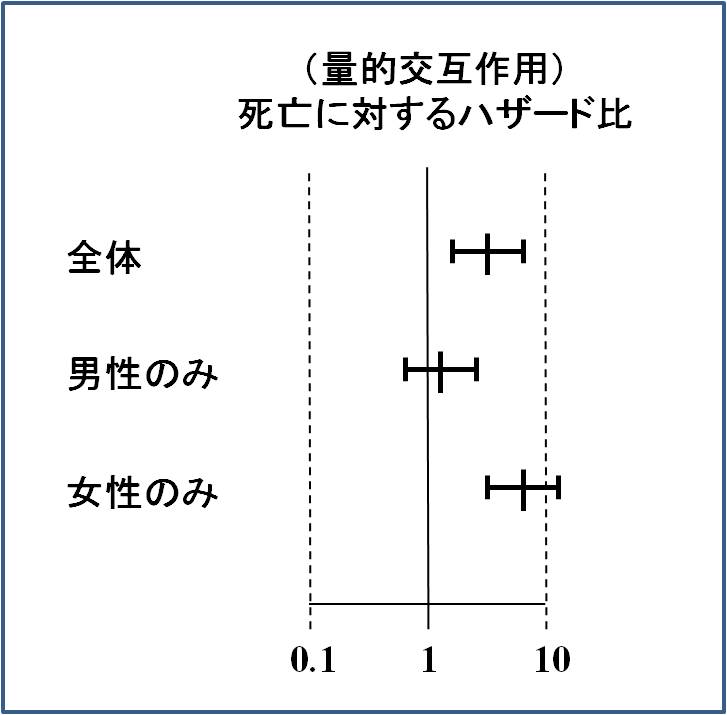
交互作用の評価方法 P for interaction、P for trendの算出
それでは実際に「Rコマンダー」を使用してこの交互作用の有無を検証してみます。
交互作用の有無は、コックスの比例ハザードモデル、もしくはロジスティック回帰分析の説明変数のモデル式に交互作用項を示す計算式である「*(アステリスク)」を追記するだけで行うことが可能です。
具体的にサンプルデータを用いてやってみます。
データには
死亡イベントの有無 Censor
死亡までの時間 Time
高血圧の有無 Hypertension (Yes or No)
ACE阻害薬による降圧治療の有無 Treatment (Yes=1 or No=0)のデータが格納されています。
まずACE阻害薬による治療の死亡イベントに対するハザード比を算出して、結果をまとめて表示すると下記のようになりました。
ハザード比 95%信頼区間 Pr(>|z|)
Treatment(全体) 0.5351 0.3902-0.7339 0.000105
Hypertension(+) 0.2947 0.1390-0.6247 0.00144
Hypertension(−) 0.6436 0.4469-0.9267 0.0178
すなわち、ACE阻害薬による降圧治療は高血圧のある患者群でより死亡抑制効果が高そうです。
量的交互作用がありそうだという結果になったということです。
では本当に交互作用が存在するのか、コックスの比例ハザードモデルで検証してみます。
治療の効果が高血圧の既往の有無によって変化するのかどうかを検討したいので、
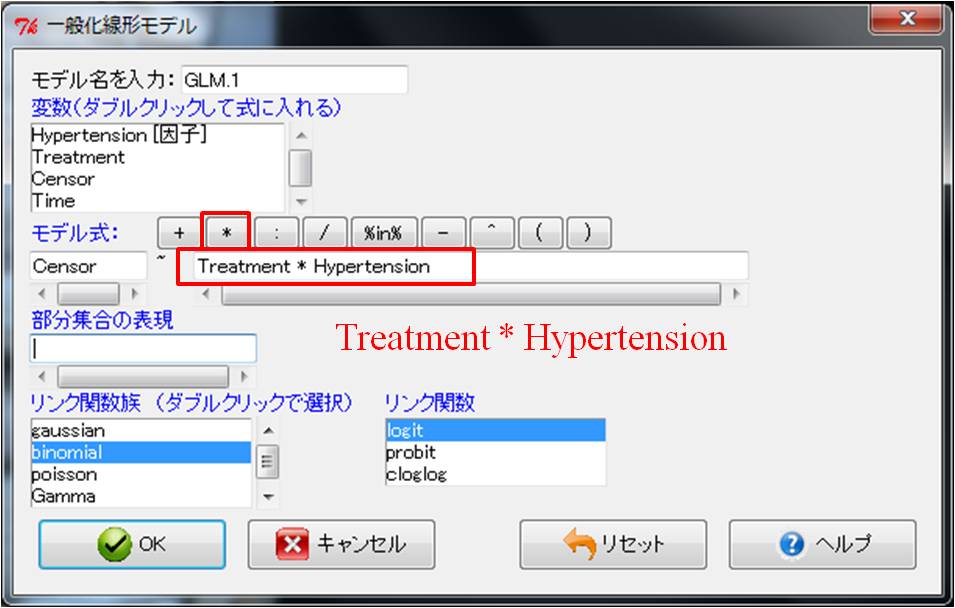
モデル式を下図のように「Hypertension * Treatment」と入力して下さい。
変数をダブルクリックすると「Hypertension+Treatment」となりますので、+の部分をアステリスクに書き換えるだけです。
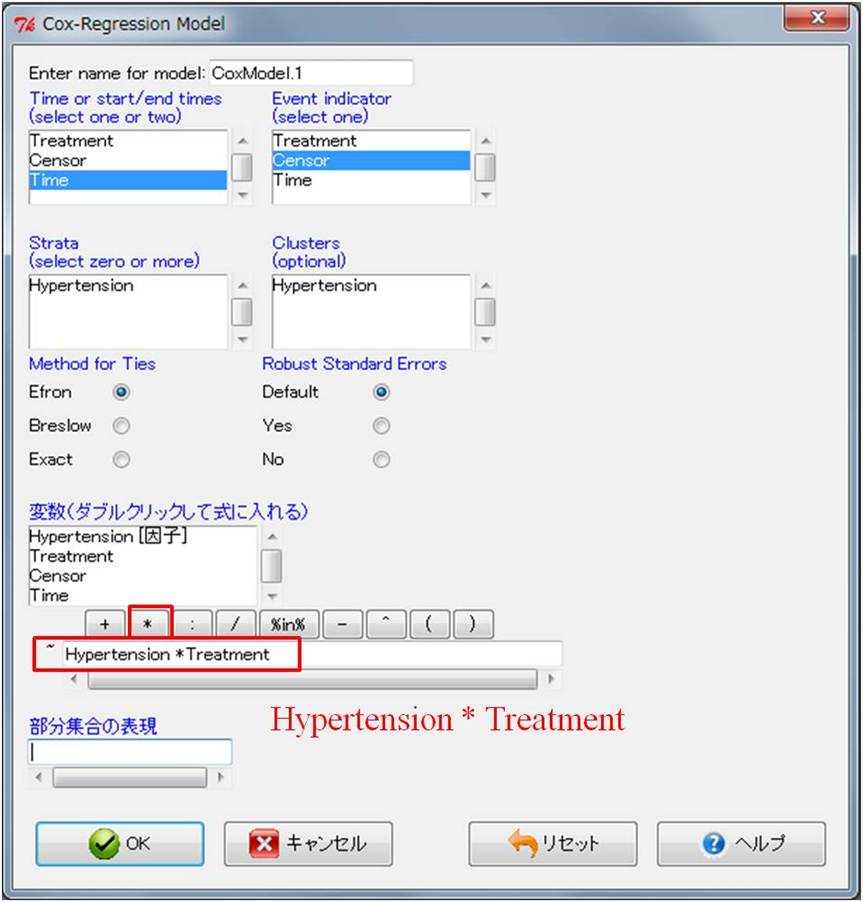
出力ウィンドウに結果が出力されました。
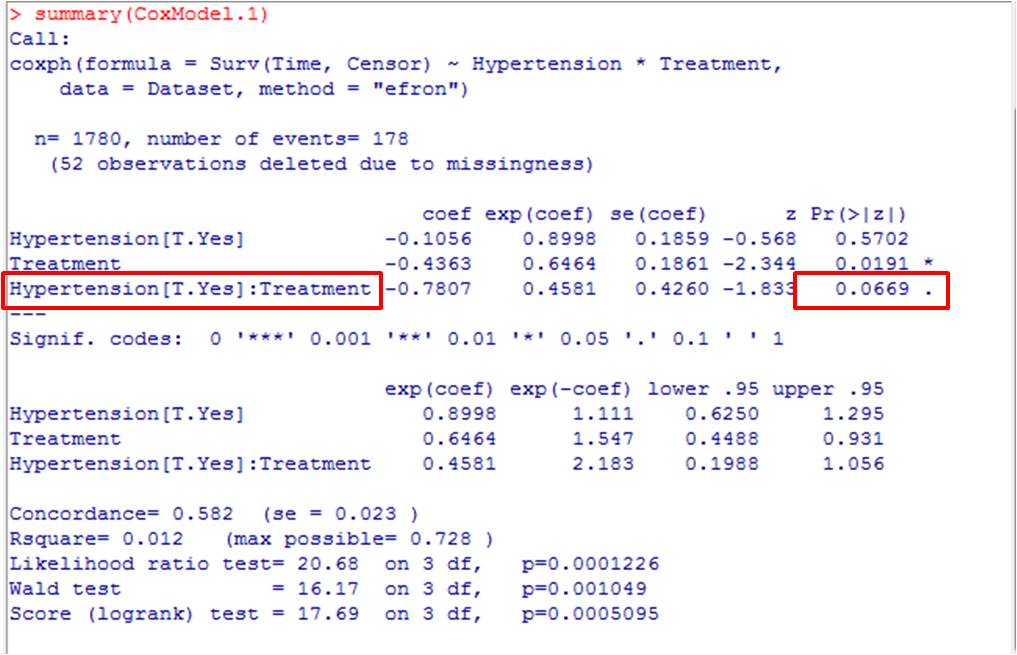
交互作用の有無は、交互作用を見たい変数がすべて記載されている列を参考にします。
このp値が、所謂 p for interaction、p for trendと呼ばれる値になります。
一般にp<0.05で、交互作用ありと判断しますが、臨床的にはp<0.1もあればほぼ交互作用ありと判断してかまわないと思います。
量的交互作用の場合も、質的交互作用の場合も見る場所は同じです。
したがって、今回の場合は p for interaction=0.0669ですので、臨床的には高血圧の有無によってACE阻害薬の治療効果に差があるといってしまってよいでしょう(交互作用があると判断します)。
ここで、もし癌の進行度といったように2つではなく複数のサブグループでの交互作用を検討したい場合は、ステージの段階を数値に置き換えて上記作業を実行します。
サブグループが複数の場合、名義変数のままでは交互作用の有無を1つのp値で算出することができませんのでご注意下さい。
なお、ロジスティック回帰分析の場合もモデル式の記入部位が異なりますが、やることは基本的に同じです。
以下の流れはコックス回帰分析の場合と同様です。