解析応用編

6. ROC曲線応用編、AUCの差の検定、NRI（net reclassification improvement）とIDI（integrated discrimination improvement）の算出方法

このサイトは無料の統計ソフトである「Ｒ」を用いて
ROC曲線の描出と各種統計量の計算
AUCの差の検定
NRI（net reclassification improvement）とIDI（integrated discrimination improvement）の算出
が実行できるように説明したサイトです。
「臨床医のためのＲコマンダーによる医学統計解析マニュアル」の読者を対象に作成しており、本書の内容を理解しているものとして解説していきます。

その他、臨床研究や英語論文執筆にご興味のある方は無料のメールマガジン
「臨床研究の立ち上げから英語論文発表までを最速最短で行うための極意」への登録も御考慮下さい。

ROC曲線応用編

「臨床医のためのRコマンダーによる医学統計解析マニュアル」ではEpiパッケージを用いた簡単なROC曲線の描出方法をご説明させて頂きました。

しかしながらより詳しい解析を行う場合に応用がきかないこと等不都合が多かったため、ここではより詳細な解析が可能な
pROCパッケージを使用した解析方法に関して記載していきたいと思います。

まずはpROCパッケージをインストールして下さい。
次にサンプルデータを使用して解析の練習を行っていきましょう。

データには心筋梗塞で入院となった患者の

年齢 Age
来院時心肺停止状態の有無 CPA（Yes=1、No=0）
院内死亡の有無 Censor（死亡＝1、生存=0）

の情報が含まれています。
個人のデータを使用する際にはエンドポイントをCensorとし、イベント有を 1、無を0に変換しておいて下さい。

次に欠損値を削除してデータセット名をwithout_missingとして下さい。

ROC曲線の描出にはまずロジスティック回帰分析を行う必要があります。
Censorを目的変数、予測に用いる変数を説明変数として ロジスティック回帰分析をGLM.1の名前で実行して下さい。
説明変数の数はいくつでもかまいませんが、ここでは説明変数としてまずAgeを使用してみましょう。

スクリプトウィンドウには
GLM.1 <- glm(Censor ~ Age, family=binomial(logit), data=without_missing)
summary(GLM.1)
のように表記されます。

さて、ここからは下記スクリプトをコピーアンドペーストしてR Console上で実行するだけです。
※回帰分析のモデル式の名前 （下記スクリプトの赤字のGLM.1の部分)は適宜変更して下さい。Windowsのアクセサリにある「ワードパッド」や「メモ帳」等のテキストエディタにコピーして編集するとすぐにRで実行しやすいです。

#####コピーアンドペースト_ここから################
library(pROC)
ROC <- roc(response=without_missing$Censor, predictor=GLM.1$fitted)
plot(1-ROC$specificities, ROC$sensitivities, xlab="1-Specificity", ylab="Sensitivity", type="l", lwd=2)
abline(a=0,b=1,lty=2) # ROC曲線の描画
CI<-ci.auc(ROC, conf.level=0.95) # AUCの信頼区間
cutoff <- coords(ROC, x="best", ret=c("threshold", "sensitivity", "specificity", "ppv", "npv"), best.method="closest.topleft")
c.point <- cutoff[1] # モデル上のカットオフ値を格納
beta<- coef(GLM.1) # ロジスティックモデルの回帰係数（対数オッズ比）を格納
cutoff.variable <- (log(c.point/(1-c.point))-beta[1])/beta[2] # 元の変量のカットオフ値を計算
#ここから結果
ROC$auc #ROC曲線の曲線下面積AUC（C統計量とも呼ばれる）
CI #曲線下面積AUCの95%信頼区間
c.point # 回帰分析モデル上のカットオフ値
cutoff.variable #説明変数が1変数の場合の最適カットオフ値（説明変数が複数ある場合は無視）
cutoff[2:5]
#sensitivityは 感度（%表記なら100倍）
#specificityは特異度（%表記なら100倍）
#ppvは陽性的中率（positive predictive value)（%表記なら100倍）
#npvは陰性的中率NPV（negative predictive value）（%表記なら100倍）
#####コピーアンドペースト_ここまで################

以上でROC曲線の描出と、様々な統計量の計算が終了しました。
結果ですが、院内死亡の有無（Censor）を予測する変数として年齢を用いた場合
ROC曲線の曲線下面積 AUC（area under the curve）= C 統計量（C statistics）は0.7318（95%信頼区間 0.7063-0.7572）
年齢のカットオフ値を69.49877歳に設定すると
感度　66.29766%
特異度　68.18182%
陽性的中率　71.96262%
陰性的中率　62.15470%
で院内死亡を予測できるということがわかりました。

AUCの差の検定

それでは次にモデル式の違いによるAUCの差の検定を行ってみます。

今回はCensorを目的変数、予測に用いる変数をAgeとCPAに設定して ロジスティック回帰分析をGLM.2の名前で実行して下さい。

スクリプトウィンドウには
GLM.2 <- glm(Censor ~ Age +CPA, family=binomial(logit), data=without_missing)
summary(GLM.2)
のように表記されます。

次に上記のスクリプトを回帰式の名前を二か所ともGLM.2に修正してからR Console上で実行して下さい。
下記スクリプトの中ではROC曲線を先ほどの図に重ね書きするためにplot( )関数の前にpar(new=T)と重ね書きを指定するスクリプトを用意し、関数内の引数としてcol="blue"で色を指定しています。

#####コピーアンドペースト_ここから################
library(pROC)
ROC <- roc(response=without_missing$Censor, predictor=GLM.2$fitted)
par(new=T)
plot(1-ROC$specificities, ROC$sensitivities, xlab="1-Specificity", ylab="Sensitivity", type="l", lwd=2, col="blue")
abline(a=0,b=1,lty=2 ) # ROC曲線の描画 col="色"で色を指定
CI<-ci.auc(ROC, conf.level=0.95) # AUCの信頼区間
cutoff <- coords(ROC, x="best", ret=c("threshold", "sensitivity", "specificity", "ppv", "npv"), best.method="closest.topleft")
c.point <- cutoff[1] # モデル上のカットオフ値を格納
beta<- coef(GLM.2) # ロジスティックモデルの回帰係数（対数オッズ比）を格納
cutoff.variable <- (log(c.point/(1-c.point))-beta[1])/beta[2] # 元の変量のカットオフ値を計算
#ここから結果
ROC$auc #ROC曲線の曲線下面積AUC（C統計量とも呼ばれる）
CI #曲線下面積AUCの95%信頼区間
c.point # 回帰分析モデル上のカットオフ値
cutoff.variable #説明変数が1変数の場合の最適カットオフ値（説明変数が複数ある場合は無視）
cutoff[2:5]
#sensitivityは 感度（%表記なら100倍）
#specificityは特異度（%表記なら100倍）
#ppvは陽性的中率（positive predictive value)（%表記なら100倍）
#npvは陰性的中率NPV（negative predictive value）（%表記なら100倍）
#####コピーアンドペースト_ここまで################

今回は、院内死亡の有無（Censor）を予測する変数として年齢と来院時心肺停止状態の有無の情報をを用いたわけですが、さきほどと異なり
ROC曲線の曲線下面積 AUC（area under the curve）= C 統計量（C statistics）は 0.7627（95%信頼区間 0.7387-0.7866）
回帰分析モデル上のカットオフ値を0.5581395 に設定すると
感度　67.15867%
特異度　71.36364%
陽性的中率　74.28571%
陰性的中率　63.82114%
で院内死亡を予測できるということがわかりました。
すべての予測精度が上昇していることがわかりますね。

それではこのGLM.1とGLM.2を使ったROC曲線のAUCの差を検討してみます。
下記スクリプトをコピーアンドペーストしてR Console上で実行して下さい。
※回帰分析のモデル式の名前 （下記スクリプトの赤字のGLM.1とGLM.2の部分)は適宜変更して下さい。

#####コピーアンドペースト_ここから################
ROC1 <- roc(response=without_missing$Censor, predictor=GLM.1$fitted)
ROC2 <- roc(response=without_missing$Censor, predictor=GLM.2$fitted)
roc.test(ROC1, ROC2, method="delong", alternative="two.sided")
#####コピーアンドペースト_ここまで################




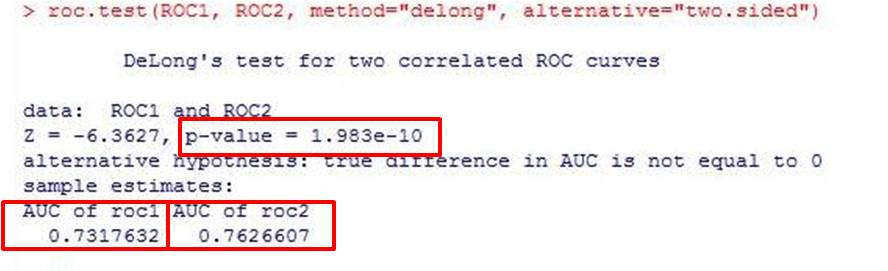
結果ですが、先ほど求めたとおり
モデル式1の曲線下面積AUC = C 統計量 が0.7317632
モデル式2の曲線下面積AUC = C 統計量 が0.7626607
p=1.983×10^-10
と、統計学的有意にAUCに差があるという結果が得られました。

NRI（net reclassification improvement）と
IDI（integrated discrimination improvement）の算出方法

これまでは診断精度やイベントの予測精度の代表値として、上記のようにROC曲線のAUCの値が用いられてきました。
すなわち、上記のようにAUCの差を検討し有意差がでた場合、例えば
「AgeにCPAの情報を追加することでイベントの予測精度が上昇した」というように論文に記載されていました。
しかし、近年このAUCを診断精度や予測精度の代表値として使用するという考え方があまり正確ではないというように認識されるようになってきており、その変わりとして提唱されている概念が

NRI（net reclassification improvement）と
IDI（integrated discrimination improvement）

ということになります。
すなわち、NRI（net reclassification improvement）とIDI（integrated discrimination improvement）は、
計算した「モデル式がどれだけうまく予測したいイベントを場合分けできるか」を、より正確に表した概念になります。

まだこの概念が提唱されてからそれほど時間がたっておらず、残念ながら適当な日本語はありません。

算出方法自体は非常にシンプルです。

まずはPredictABELというパッケージの読み込みを行っておいて下さい。

次に、上記のROC曲線応用編で行ったように、比較したいROC曲線のモデル式を2つロジスティック回帰分析で計算しておきます。
すなわち、GLM.1とGLM.2を計算しておいて下さい。

後は 下記スクリプトをコピーアンドペーストしてR Console上で実行するだけです。
なお、赤字のcOutcome=3の数字はCensorの情報がwithout_missingのデータセットの何列目にあるかを指定する数字です。
今はデータセットの3列目にありますので3としておりますが、この数値も適宜変更して下さい。
また、後述するReclassification Tableの算出に当たって、Tableの分割ポイントはGLM.1$fittedの4分位に設定しています。
GLM.1$fittedには各患者のイベントが生じる確率が格納されています。
この分割ポイントも青字のスクリプトの部分をcutoff<-c(0, 0.5, 1)等のように修正して自分で設定することが可能です。
c ( )内に、任意の変換点の数値を半角英数字で記載して、コンマ「,」で繋げます。小数点はピリオド「.」で表記です。変換点はいくつあっても問題ありません。

#####コピーアンドペースト_ここから################
library(PredictABEL)
predRisk1 <- GLM.1$fitted
predRisk2 <- GLM.2$fitted
value<-as.vector(quantile(GLM.1$fitted))
cutoff <- c(0,value[2],value[3],value[4],1)
reclassification(data=without_missing, cOutcome=3, predrisk1=predRisk1, predrisk2=predRisk2, cutoff=cutoff)
#####コピーアンドペースト_ここまで################

出力結果をみてみましょう。



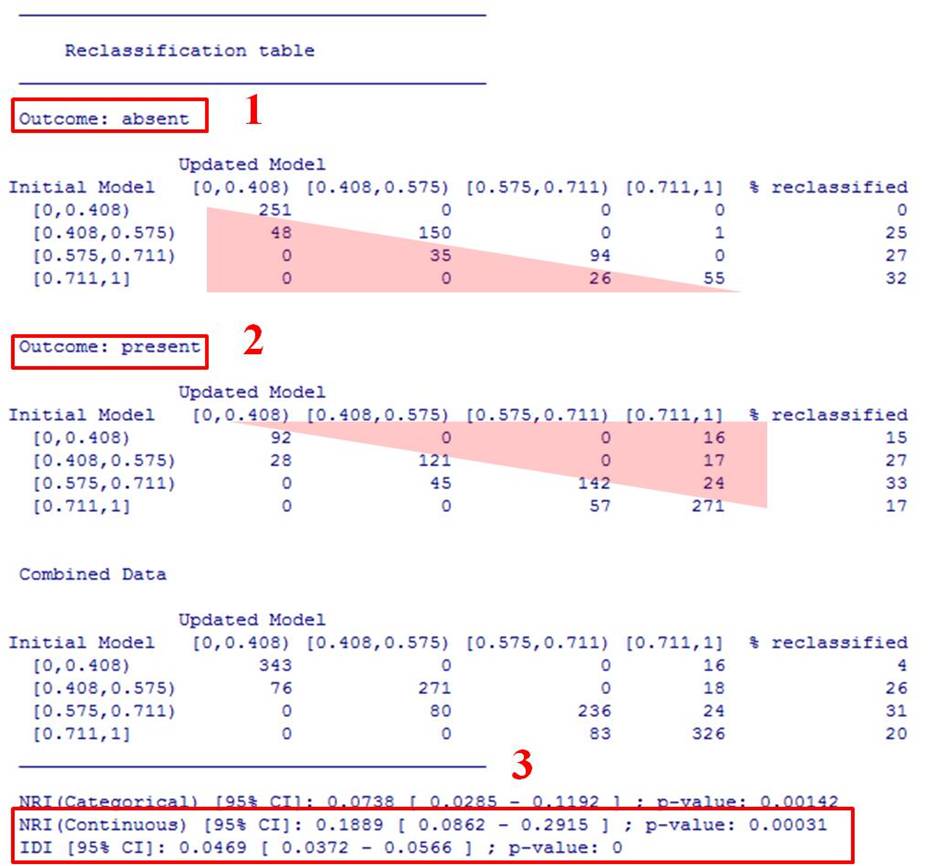
まずはReclassification Tableの1と2に目を通します。
Table 1ではOutcome: absentと記載されています。これはCensorが0の患者のみのデータになり、各モデル式で推定した患者の分布が分割表の形で出力されています。
すなわち、Table 1の行にはInitial Modelと記載があり、これはモデル式1で、Table 1の列にはUpdated Modelと記載があり、これはモデル式2で推定したイベント発生確率の患者数が記載されています。
イベントがなかった患者群のみの分割表であるため、モデル式1よりもモデル式2の方が予測精度が高い場合、患者はピンクで色付けしたように左下に再分類されることになります。
例えばTable 1では、イベント発生確率がInitial Modelで0.408-0.575（40.8%-57.5%）であった患者の内、48名がUpdated Modelでイベント発生確率0-0.408（0%-40.8%）に、より正確に再分類されているということです。
すなわち、左下に数値がたくさん記載されているほど、モデル式2の方が予測精度が優れているということを意味します。

同様に、Table 2ではOutcome: presentと記載されています。これはCensorが1の患者のみのデータの分割表になりますので、先ほどとは逆に、右上に数値がたくさん記載されている程モデル式2の方が予測精度が優れているということを意味します。

これらの結果を数値で表現したものが

NRI（net reclassification improvement）と
IDI（integrated discrimination improvement）

ということになります。

論文や発表では、このReclassification TableとNRI、IDIの数値を提示すればよいと思います。
具体的な数値は図中の3を参照して下さい。
なお、NRIはContinuousと記載のある部分を参考にして下さい。
というのも、実はNRIはcutoffに指定するカテゴリー区分によって結果が変わってしまうためです。
NRI(Categorical)は値が一定していないということです。
この問題を回避するため、すなわちカテゴリー区分に結果が依存されないようにNRI(Continuous)が考えられたという経緯があります。
したがって、一般的にはNRI(Continuous)の部分のみに注目して判断するように推奨しております。

NRIもIDIもp値が0.05未満の場合、新しいモデル式の予測精度の方が古いモデル式よりも優れていると判断します。

すなわち、今回の結果は

NRIは0.1889 (95%信頼区間 0.0862 - 0.2915 ）、 p-value= 0.00031
IDIは0.0469 （95%信頼区間 0.0372 - 0.0566 ）、 p-value= 0

で、モデル式2の方が有意にイベント予測精度が高かった
というように記載します。

ここで注意して頂きたいのですが、多くの医学論文でこのNRIとIDIは%表記（上記の場合NRI 18.89%、IDI 4.69%）されていますがこれは誤用と判断される場合があるということです。

NRIとIDIは、%表記ではなくそのままの数値を提示するようにして下さい。

より詳細に確認したい方はコチラの論文をご参照下さい。