解析応用編

4. CART（カート）classification and regression treeを用いた解析方法

このサイトは無料の統計ソフトである「Ｒ」を用いて
CART（カート） classification and regression tree
を実行できるように説明したサイトです。
「臨床医のためのＲコマンダーによる医学統計解析マニュアル」の読者を対象に作成しており、本書の内容を理解しているものとして解説していきます。

その他、臨床研究や英語論文執筆にご興味のある方は無料のメールマガジン
「臨床研究の立ち上げから英語論文発表までを最速最短で行うための極意」への登録も御考慮下さい。

survival CART（カート）classification and regression treeを用いた解析方法

survival CARTはバイオマーカー等の連続変数でTime-to-eventのイベント率を予測する際に、適したカットオフ値を推測するのに有用な方法です。
ここでは専用のsurvival_CART_dataのエクセルデータを使用して説明します。

このデータ内ではバイオマーカーとしてN末端プロ脳性ナトリウム利尿ペプチド N terminal pro-brain natriuretic peptide（NTproBNP）のデータを、Time-to-eventとして心不全による入院のデータを用いています。時間軸の単位は日数で、それぞれのデータが3000人分利用可能です。
NTproBNPは心不全に関わるバイオマーカーで、値が高くなるほど心臓に負荷がかかっていることを意味し、心不全イベントが生じやすくなると予想できます。

一般にバイオマーカー等の連続変数の値と予後の関係を推測する場合、連続変数の値を3分位や4分位でカテゴリー化して各群におけるイベント率を比較することが多いと思います。

例えば練習用のsurvival_CART_data内のNTproBNP値を4分位でカテゴリー化して心不全入院回避率曲線を描いてみます（p24、p34、p102）。
NTproBNPの4分位は
0% 　　　　25%　　　　 50%　　　　 75%　　　　 100%
1.330　　 206.725　　 489.250　　 1077.000　 190116.000
ですので、NTproBNPの数値が0-25%の患者をquartile1、25-50%の患者をquartile2、50-75%の患者をquartile3、75-100%の患者をquartile4にグループ分けします。
各グル―プの心不全入院回避率曲線を描くと下図のようなりました。


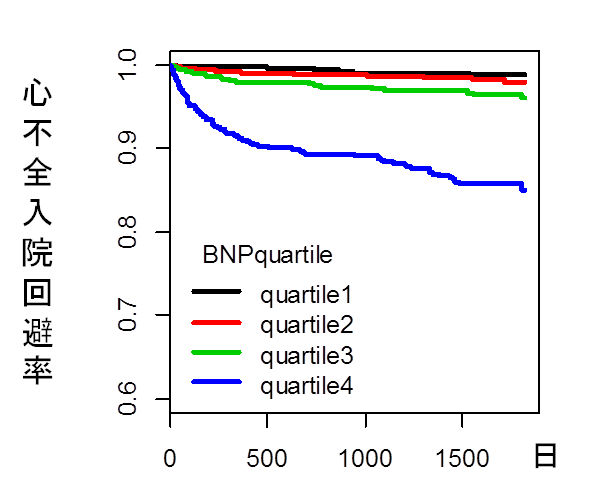
どうやらNTproBNPを4分位でグループ分けした場合、第4四分位の患者群で突出して予後が悪いことが見て取れます。
ここで疑問が生じます。この4分位で分ける方法で本当にうまく心不全入院回避率曲線の違いを検出できているのでしょうか？
survival CARTでは統計学的にイベント曲線の変換を生じるような連続変数の値を算出してくれます。

それでは実際に検定を行いましょう。
まず準備です。
バイオマーカー等の連続変数、Time-to-eventデータのみのデータセット（3列）を作成して下さい。
次に連続変数の変数名をVariable、Time-to-eventデータの変数名をCensor、Timeとし、欠損データを取り除いてwithout_missingというデータセットを作成して下さい(p87）。
「party」というパッケージを読み込んでください（p8）。

最後に下記スクリプトをＲ Consoleにコピーアンドペーストして実行して下さい。

#####コピーアンドペースト_ここから################
#survival CART
library(party)
survivalCART<- ctree(Surv (without_missing$Time, without_missing$Censor)~without_missing$Variable, data=without_missing)
plot(survivalCART)
#####コピーアンドペースト_ここまで################

下記の結果が得られました。
すなわち、NTproBNPで心不全回避率を予測したい場合、NTproBNP値が1913 pg/mLを境にしてもっともイベント率に差が生じるようです。次に1049 pg/mL、442.9 pg/mLと分岐が続きます。


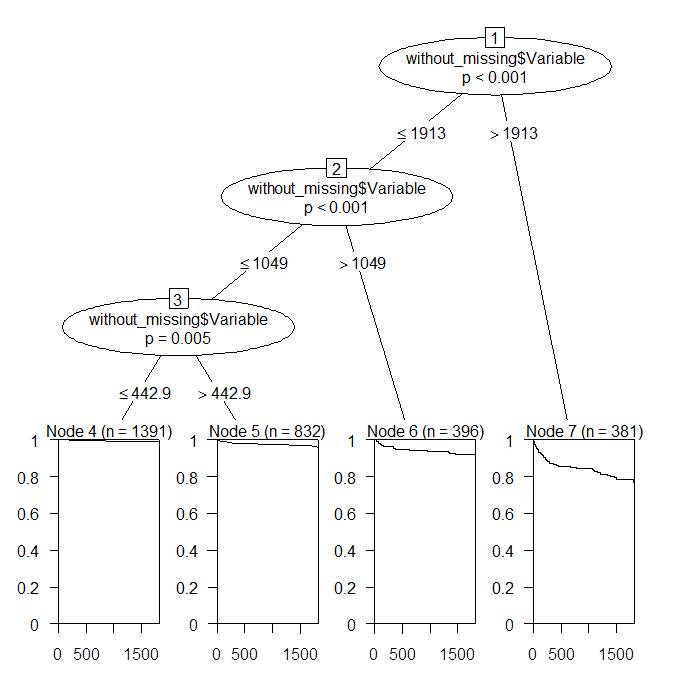
4分位で分類した際にはNTproBNP 1077 pg/mL以上の患者群をいっしょくたにして解析していましたが、survival CARTを行うことによって1077 pg/mL以上でもさらに1913 pg/mLを境にしてイベント率がかなり異なるということがわかりました。

最初に述べたとおり、survival CARTがバイオマーカー等の連続変数でTime-to-eventのイベント率を予測する際に、適したカットオフ値を推測するのに有用な方法であることがわかっていただけたと思います。

ただし、データによってはそもそも第一分岐すら行われない場合もあります。
そのような場合には設定した予測変数の違いによって統計学的にうまくイベントの違いを検出できないということになりますので、これまで通りの方法で4分位や3分位点を用いて探索的に解析を行っていく他ありません。

また、survival CARTで得られる図は非常に大きくなることがあります。
R Graphicsの画面が小さいと文字や図がつぶれてしまい何を見ているのかわからなくなってしまいますので、そのような場合はあわてずにR Graphicsの表示範囲を拡大して下さい。

CART（カート）classification and regression treeを用いた解析方法

survival CARTではエンドポイントとしてTime-to-eventのデータを用いましたが、もちろん院内死亡や合併症発症の有無といったようにエンドポイントに時間情報を含まない場合もCARTを行うことが可能です。

その場合、ctree内の式が少し変更になるだけです。
先ほどのデータでVariableとCensorの情報のみを用いてCARTを実行してみましょう。

下記スクリプトをＲ Consoleにコピーアンドペーストして実行して下さい。

#####コピーアンドペースト_ここから################
#CART
library(party)
CART<- ctree(as.factor(without_missing$Censor) ~ without_missing$Variable, data=without_missing)
plot(CART)
#####コピーアンドペースト_ここまで################

下記の結果が得られました。
解釈の仕方はsurvival CARTの時と同じです。
生存曲線が、単純なイベント発生率になっているだけです。